Úloha: Zotriedenie spojáku

1. Napíšte si vlastnú deklaráciu spojáku, s ktorou budete pracovať
2. Napíšte procedúru sort, ktorá zotriedi spojový zoznam vzostupne (od najmenšej hodnoty po najväčiu).

Poznámky:

1. Triedenie by malo mať časovú zložitosť maximálne \( O(n^2) \), kde n je počet prvkov v spojáku.
2. Nepíšte žiadny inicializačný kód spojáku, stačí len správna definícia a samotná procedúra sort.
3. Triedenie naimplementuje len s pomocou spojového zoznamu, tzn. žiadne riešenia typu skopírujem si spoják najprv do pola nevymýšlajte.

Tento text je určený len pre tých, ktorí sa rozhodli písať svoj zápočťák v Jave.

Maven

Maven je buildovací nástroj pre Javu, ktorý umožňuje oddeliť buildovanie projektu od samotného IDE. Čo veľmi uľahčuje druhej osobe, zbuildovať aký koľvek projekt u seba a jeho následné spustenie bez toho, aby si inštaloval vaše IDE alebo si celý build nastavoval od začiatku. Veľká výhoda je, že Maven projekty viete bez problémov naimportovať do vášho obľúbeného IDE, ako napr. Netbeans, Eclipse či IntelliJ.

Šablona

Pre záujemcov o Maven som pripravil jednoduchú šablonu, ktorú môžete rovno použiť. Stiahnuť si ju môžete tu.

Návod na použitie

1. Nainštalujte si Javu 8
2. Nainštalujte si Maven
3. Skúste si či Maven funguje otvorením terminálu príkazom mvn -version
4. Stiahnite šablonu projektu
5. Rozbalte šablonu
6. V terminály sa príkazom cd presuňte do koreňovej zložky projektu (obsahuje pom.xml)
7. Projekt teraz zbuildujete príkazom mvn clean package

Po zbuildovaní projektu môžete program spustiť buď príkazom:

java -jar target/project-1.0-SNAPSHOT.jar

alebo príkazom:

java -cp target/project-1.0-SNAPSHOT.jar cz.cuni.HelloWorld

Ak je všetko v poriadku, tak by ste mali vidieť tento výstup:

Hello World!

V súbore pom.xml môžete zmeniť:

• verziu javy
• triedu obsahujúcu metódu main, tak aby fungoval prvý z príkazov vyššie

Ak všetko funguje, tak len jednoducho nakopírujte vaše zdrojové kódy do zložky src/main projektu a ste hotový. Potom už iba otvorte tento projekt vo vašom obľúbenom IDE, všetky by mali bez problémov podporovať Maven projekty.

Na poslednej hodine sme si zaviedli ukazatele a funkciu new, ktorá je schopná naalakovať premennú daného typu na halde. Čo sa však stane, ak naalokovanú premennú už nepotrebujeme, ako napríklad u operácii remove spojového zoznamu? Túto pamäť musíme ručne uvolniť (dealokovať) funkciou dispose, ktorá na vstup dostane tiež ukazateľ.

Ak však stratíme ukazateľ pred uvoľnením pamäte, tak táto časť pamäte ostane nepoužiteľná až do ukončenia programu. Takáto chyba vedie často k výnimkám typu Out Of Memory Exception (OOM), kedy si zaplníme celú haldu nepoužívanými premennými. Tomuto sa medzi programátormi hovorí tiež leak-ovanie pamäte.

Platí nasledujúce jednoduché pravidlo: s každým zavolaním funkcie new musí byť spárované zavolanie funkcie dospose.

V letnom semestri začenete používať jazyk C#, ktorý sa o správu pamäte stará sám, tzn. žiadna funkcia dispose u neho nie je potrebná.

Binárne vyhľadávacie stromy (BST - z angl. Binary Search Tree)

Binárny vyhľadávací strom je dynamická dátová štruktúra založená na binárnom strome, v ktorom sú jednotlivé prvky (uzly) usporiadané tak, aby v ňom bolo možné rýchlo vyhľadávať. Tento strom má nasledujúce vlastnosti:

• každý uzol má maximálne 2 potomkov - ľavého a pravého syna
• každý uzol obsahuje hodnotu alebo kľúč, ktorý chceme vyhľadávať a určuje usporiadanie uzlov
• pre každý uzol v strome platí, že ľavý resp. pravý podstrom obsahuje len kľúče menšie resp. väčšie než je kľúč aktuálneho uzlu

Základné operácie BST:

• insert - vloženie nového prvku
• member - zistenie či sa prvok s danou hodnotou nachádza v strome
• delete - odstránenie prvku zo stromu

Pekná vizualizácia fungovania BST tu.

Na zamyslenie:

• Aká je časová zložitosť operácií insert, delete, member?
• Ako súvisí binárne vyhľadávanie v zotriedenom poli s BST?

Prehľadávanie stromu do hĺbky

Podľa poradia v akom prechádzame uzly v strome môžeme definovať tieto 3 typy prehľadávania:

PREORDER

• vykonaj akciu
• prejdi ľavý podstrom
• prejdi pravý podstrom

INORDER

• prejdi ľavý podstrom
• vykonaj akciu
• prejdi pravý podstrom

POSTORDER

• prejdi ľavý podstrom
• prejdi pravý podstrom
• vykonaj akciu

Príklad:

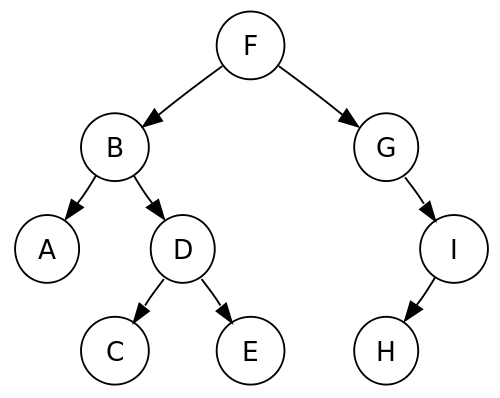
Ak definujeme akciu vypísaním hodnoty uzlu, tak dostaneme tieto výstupy:

• Inorder: A, B, C, D, E, F, G, H, I
• Preorder: F, B, A, D, C, E, G, I, H
• Postorder: A, C, E, D, B, H, I, G, F

Naimplementujte BST

Nižšie môžete vidieť jeden z možných spôsobov definovania BST v pascale. Vašou úlohou je znovu domplementovať chýbajúce základné operácie nad BST.

program bst;

type TData = integer;
     TNode = record
      data: TData;
      left: ^TNode;
      right: ^TNode;
     end;
    TBinaryTree = record
      root: ^TNode;
    end;

{ zinicializuje novy strom }
procedure init(var tree: TBinaryTree);
begin

end;

{ vykresli strom v peknom formate, napr: }
{         2
         / \
        /   \
       /     \
      /       \
     7         5
    / \         \
   /   \         \
  2     6         9
 / \             /
5   8           4  
}
procedure pretty_print(var tree: TBinaryTree);
begin

end;

{ vlozi novy prvok do stromu }
procedure insert(var tree: TBinaryTree; val: TData);
begin

end;

{ vrati true ak sa dany prvok v strome nachadza inak false }
function member(var tree: TBinaryTree; val: TData): boolean;
begin

end;

{ odstrani dany prvok zo stromu (pouzite spravne dispose!)}
procedure remove(var tree: TBinaryTree; val: TData);
begin

end;

{ vrati pocet uzlov v strome }
function size(var tree: TBinaryTree): integer;
begin

end;

{ zmaze cely strom (pouzite dispose!) }
procedure delete(var tree: TBinaryTree);
begin

end;

{ vypise hodnoty uzlov v strome v preorder poradi }
procedure print_preorder(var tree: TBinaryTree);
begin

end;

{ vypise hodnoty uzlov v strome v inorder poradi }
procedure print_inorder(var tree: TBinaryTree);
begin

end;

{ vypise hodnoty uzlov v strome v inorder poradi }
procedure print_post(var tree: TBinaryTree);
begin

end;

Bonusová domáca úloha

Hlavne pre tých, čo nemajú dosť bodov z domácich úloh.

Doimplementujte všetky operácie nad BST definovaných vyšše.

Termín odovzdania: 4. 1. 2017 (23:59)

Spôsob odovzdania: zdrojový kód mailom

Počet bodov: 50

Doteraz sme používali len statické premenné a preto sme napríklad vždy pracovali len s konštantne veľkým poľom. Ako sme si povedali už minule, statické premenné sa alokujú na zásobník (stack) a veľkosť týchto premenných musí byť známa už počas kompilácie. Vo väčšine prípadov však velkosť potrebných dátových štruktúr (napr. pole) nevieme. V takom prípade musíme siahnuť po dynamických premenných, ktoré sa alokujú na haldu (heap). Práca s týmito premennými je však o niečo komplikovanejšia, viz. príklady nižšie.

Statické premenné

Toto je štandardný prístup k premenným, ktorý už poznáte:

var a,b: integer;
begin
  a := 10;
  b := 10;
  writeln(a);
  writeln(b);
end.

Výstup:

10
10

Pamäť programu vyzerá potom nasledovne:

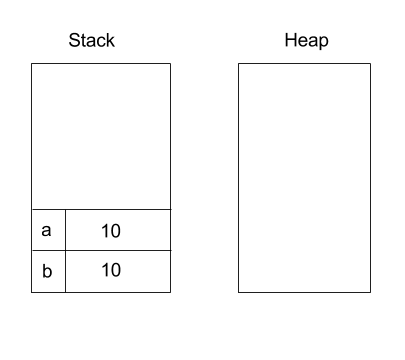
Dynamické premenné

Prístup k premenným cez ukazovatele (pointre).

var n: ^integer; { ukazatel na integer}
    address: ^word;
begin
  new(n); { zinicializujeme novy integer na halde }
  n^ := 10; { do premennej priradime hodnotu 10}

  { ziskame adresu premennej n, tzn. kam ukazuje}
  address := addr(n);
  writeln(address^);

  { ziskame hodnotu premennej n}
  writeln(n^);
end.

Výstup:

12336
10

Pamäť programu vyzerá nasledovne:

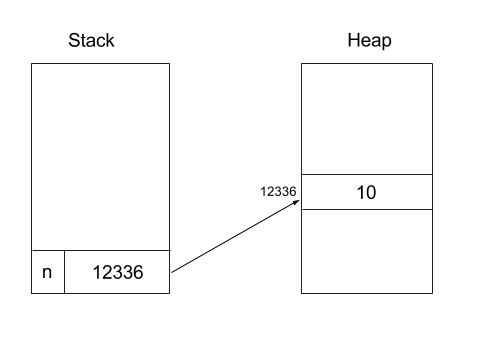
V tomto príklade sme použili nový operátor ^, ktorý sa používa jednak k deklarovaniu premennej typu ukazateľ na daný typ (napr. ukazateľ na integer) a druhak k prístupu k hodnote na adrese ukazateľa (tomu sa hovorí aj dereferencovanie ukazateľa).

Taktiež sme použili funkciu new, ktorá alokuje na halde premennú typu daného ukazateľa.

Poznámka: Správne by sa mali premenné po použití ešte dealokovať a uvolniť tým miesto na halde, ale to zatiaľ robiť nebudeme.

Úlohy

Dynamické premenné sa dajú použiť k vytváraniu dynamických dátových štruktúr ako napr. spojového zoznamu (linked list). Spojový zoznam je zložený z uzlov, kde každý uzol obsahuje ukazatel na svojho nasledovníka.

Štruktúra spojového zoznamu v pamäti môže vyzerať nejak takto:

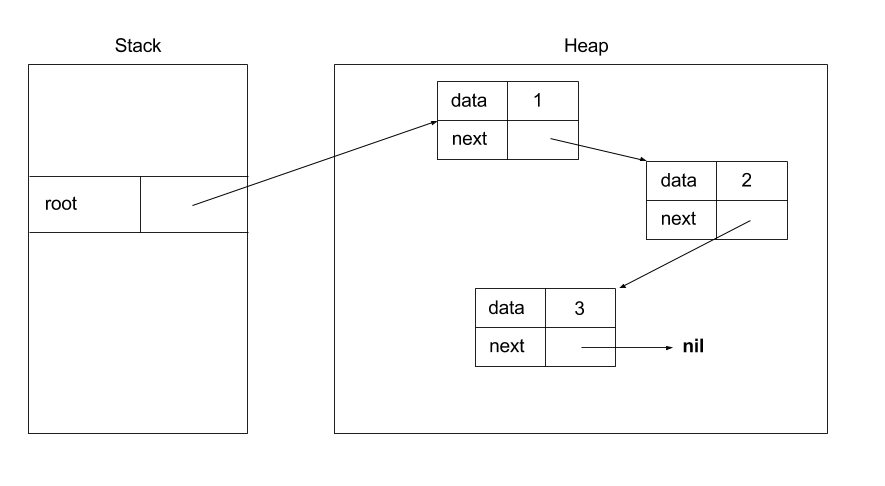
Ukazatel, ktorý neukazuje nikam sa definuje tak, že sa doňho priradí hodnota nil.

Naimplementujte spojový zoznam

Nižšie môžete vidieť jeden z možných spôsobov definovania spojáku v pascale. Vašou úlohou je domplementovať chýbajúce základné operácie nad spojákom.

program linked_list;

type TData = integer; { typ dat, ktore budeme ukladat do spojaku }
     TNode = record   { jeden uzol spojaku }
      data: TData;
      next: ^TNode;
     end;
    TLinkedList = record  { samotny spojak }
      root: ^TNode;
    end;

{ zinicializuje prazdny spojak }
procedure init(var list: TLinkedList);
begin

end;

{ vypise hodnoty v spojaku na jeden riadok }
procedure print(var list: TLinkedList);
begin

end;

{ vlozi prvok na koniec spojaku }
procedure append(var list: TLinkedList; val: TData);
begin

end;

{ vlozi prvok na zaciatok spojaku }
procedure prepend(var list: TLinkedList; val: TData);
begin

end;

{ odstrani prvy vyskyt daneho prvku zo spojaku }
procedure remove(var list: TLinkedList; val: TData);
begin

end;

{ zisti ci sa dany prvok nachadza v spojaku }
function member(var list: TLinkedList; val: TData): boolean;
begin

end;

{ vrati dlzku spojaku, tj. pocet prvkov, ktory obsahuje }
function length(var list: TLinkedList; val: TData): integer;
begin

end;

{ spoji 2 spojaky do jedneho (lubovolnym sposobom) }
procedure concat(var list1, list2, output: TLinkedList);
begin

end;

{ zaradi prvok na vhodne miesto tak, aby vysledny spojak
  bol zotriedeny, predpoklada, ze spojak na vstupe je uz zotriedeny }
procedure insertSorted(var list1: TLinkedList; val: TData);
begin

end;

{ zleje 2 zotriedene spojaky do jedneho zotriedeneho spojaku }
procedure merge(var list1, list2, output: TLinkedList);
begin

end;

var list: TLinkedList;

begin
  { ... }
end.

Domáca úloha

Vašou domácou úlohou tentokrát je doimplemetovanie všetkých operácii nad spojovým zoznamom definovaným vyšše.

Termín odovzdania: 20. 12. 2016 (23:59)

Spôsob odovzdania: zdrojový kód mailom

Počet bodov: 40

Zásobník (stack) a fronta (queue) sú jedny zo základných dátových štruktúr, ktoré sa používaju k dočasnému ukladaniu dát. Tieto štruktúry taktiež určujú poradie spracovávania dát, ktoré obsahujú.

Z fronty dáta vystupujú v rovnakom poradí, v akom do nej vstúpili. Takejto štruktúre sa bežne hovorí FIFO - First In First Out. V podstate funguje rovnako ako fronta v obchodoch :).

Zo zásobníku naopak vystupujú vždy najprv dáta, ktoré doň boli vložené naposledy. Takejto štruktúre sa zas hovorí LIFO - Last In First Out. Predstavte si dieru, do ktorej postupne hádžete nejaké veci, vždy keď z nej chcete niečo vybrať, tak musíte začat najprv vecou, ktorá sa práve nachádza na vrchu.

Použitie: prehľadávanie grafov alebo stavového priestoru, vyhodnocovanie aritmetických výrazov atď.

Zásobník

Na vytvorenie zásobníku potrebujete len nejaký zoznam alebo pole, do ktorého si budete ukladať jednotlivé prvky a nejakú premennú, v ktorej si budete udržovať aktuálny počet uložených prvkov. Nad touto dátovou štruktúrou potom musíte definovať operácie, ktoré budú dodržovať vlastnosti zásobníku.

Ako môže vyzerať zásobník napr. v Pascale:

program stack;

{ znovu budeme predpokladat, ze nas zasobnik nebude obsahovat viac
  nez nejaky konstanty pocet prvkov }
const MAX = 1000;

type TData = char; { typ dat ktore budeme do zasobniku vkladat}

{ Na reprezentaciu zasobniku pouzijeme typ record (struktura),
  ktora sa pouziva na zoskupovanie niekolkych premennych.
  K jednotlivm premennym sa potom dostaneme pomocou .
  Napr. var rec: TStack;
        rec.size = 10; }
type TStack = record   
  items: array[1..MAX] of TData; { obsah zasobniku}
  size: 0..MAX;                  { pocet prvkov v zasobniku }
end;

{ vrati True ak je zasobnik prazdny, inak False }
function isEmpty(var stack: TStack): boolean;

{ zinicializuje prazdny zasobnik}
procedure init(var stack: TStack);

{ vlozi jeden prvok na vrch zasobniku }
procedure push(var stack: TStack; item: TData);

{ vráti prvok z vrchu zasobnika (ale neodstrani) }
function peek(var stack: TStack): TData;

{ vrati a odstrani prvok z vrchu zasobnika }
function pop(var stack: TStack): TData;

Poznámka: Fronta by sa dala reprezentovať úplne rovnako, akurát by bolo treba trochu upraviť implementáciu procedúr push a pop.

Úloha 1: Naimplementujte si zásobník

Doimplementujte funkcie a procedúry z príkladu vyššie.

Úloha 2: Uzátvorkovanie druhýkrát

Napíšte funkciu checkParenthesis, ktorá skontroluje, že uzátvorkovanie vstupného reťazca je správne. Reťazec tentokrát môže obsahovať až 3 typy zátvoriek: ()[]{} a otvorená zátvorka jedného typu môže byť ukončená len opačnou zátvorkou rovnakého typu. Na riešenie úlohy použite zásobník z predchádzajúcej úlohy.

Príklady:

Vstup: '{()}[]'
Výstup: True

Vstup: '{()][]'
Výstup: False

Vstup: '{()[]'
Výstup: False

Prefixový vs infixový vs postfixový zápis aritmetického výrazu

Bežnému vyjadreniu aritmetických výrazov napr.:

 (5 + ((1 + 2) * 4)) 

sa hovorí infixový zápis, pretože operátor sa vždy nachádza medzi (in) operandami. Alternatívne môžme ten istý výraz vyjadriť v postfixovom zápise ako:

 5 1 2 + 4 * +  

alebo v prefixovom zápise ako:

 + 5 * + 1 2 4 

Prefixový alebo postfixový zápis je narozdiel od infixového jednoznačný a preto u nich odpadáva potreba definovať prioritu operátorov alebo zátvorky. To samozrejme zjendodušuje ich strojové spracovanie.

Prefixovému zápisu sa tiež hovorí poľská notácia.

Bonusová úloha: Vyhodnotenie výrazu v poľskej notácii

Napíšte funkciu evalExpression, ktorá dostane na vstup výraz v poľskej notácii ako reťazec a ona vráti jeho hodnotu. Napr.: pre vstup + 1 2 vráti hodnotu 3.

Hint: Použite zásobník :)

Počet bodov: 20

Odovzdanie: mailom do 6. 13. 2016 (23:59)

Prehľadávanie grafu

Z prednášky by ste už mali vedieť čo je to prehľadávanie do širky - Breadth-first search (BFS) a prehľadávanie do hĺbky - Depth-first search (DFS).

Pre pripomenutie:

BFS:

DFS:

Vezmime si tento pseudokód prehľadávania grafu:

graph - nejaka reprezentacia grafu
root - vrchol v ktorom zacneme prehladavanie

{ inicializacia pomocnych premennych }
for each node n in graph:
    { u kazdeho vrcholu si poznacime ci sme ho uz videli }
    n.visited := False  

c := empty Collection { prazdna kolekcia ktoru si este dodefinujeme }

root.visited := True
push(c, root)                      

while not isEmpty(c):        
    current := pop(c)
    for each node n that is adjacent to current:
        if not n.visited:
            n.visited := True
            push(c, n)

Aké prehľadávanie dostaneme, ak si za Collection dosadíme zásobník a aké ak frontu?

Domáca úloha

V CodEx-e nájdete svoju domácu úlohu: Kyblík.

Hint: Použite napr. prehľadávanie do šírky.

Poznámka: Tentokrát máte vstup načítať zo súboru bitmap.in, nie zo štandardného vstupu. Pre prácu so súbormi viz. Cvičenie č. 4.

Termín odovzdania: 13. 12. 2016 (23:59)